Co když vaše data NEJSOU normální?

Úvod

Tento týden je Halloween a my, datoví geekové, se v přestávkách mezi triky a pamlsky pochechtáváme nad tímto roztomilým memem přes sociální sítě.

Myslíte, že je to vtip? Řeknu vám, že to není k smíchu. Je to děsivé, věrné duchu Halloweenu!“

Pokud nemůžeme předpokládat, že většina našich dat (obchodního, společenského, ekonomického nebo vědeckého původu) je alespoň přibližně „normální“ (tj. že jsou generována Gaussovým procesem nebo součtem více takových procesů), pak jsme ztraceni!

Tady je extrémně stručný seznam věcí, které nebudou platit,

• Celá koncepce six-sigma
• Slavné pravidlo 68-95-99,7
• „Svatý“ pojem p=0,05 (vychází z intervalu 2 sigma) ve statistické analýze

Je to dost děsivé? Pojďme si o tom říci více…

Všemocné a všudypřítomné normální rozdělení

Nechme tuto část stručnou a milou.

Normální (Gaussovo) rozdělení je nejznámějším rozdělením pravděpodobnosti. Zde je několik odkazů na články popisující jeho sílu a širokou použitelnost,

• Proč datoví vědci milují Gaussovo

• Jak ovládnout statistickou část pohovoru o datových vědách
• Co je tak důležité na normálním rozdělení?

Díky svému výskytu v různých oblastech a centrální limitní větě (CLT) zaujímá toto rozdělení ústřední místo v datové vědě a analytice.

V čem je tedy problém?

To je všechno hezké, v čem je tedy problém?“

Problém spočívá v tom, že často můžete pro svůj konkrétní soubor dat najít rozdělení, které nemusí splňovat normalitu, tj. vlastnosti normálního rozdělení. Ale kvůli přílišné závislosti na předpokladu Normality je většina rámců pro podnikovou analýzu přizpůsobena pro práci se sadami dat s Normálním rozdělením.

To je téměř zakořeněno v našem podvědomí.

Řekněme, že jste požádáni o detekční kontrolu, zda má nová dávka dat z nějakého procesu (inženýrského nebo obchodního) smysl. Pod pojmem „dává smysl“ rozumíte, zda nová data patří, tj. zda jsou v „očekávaném rozsahu“.

Co je to „očekávání“? Jak tento rozsah kvantifikovat?

Automaticky, jakoby řízeni podvědomou pohnutkou, změříme průměr a směrodatnou odchylku výběrového souboru dat a pokračujeme v kontrole, zda nová data spadají do určitého rozsahu směrodatných odchylek.

Pokud máme pracovat s 95% hranicí spolehlivosti, pak jsme rádi, že data spadají do 2 směrodatných odchylek. Pokud potřebujeme přísnější hranici, zkontrolujeme 3 nebo 4 směrodatné odchylky. Vypočítáme Cpk, nebo postupujeme podle směrnic six-sigma pro úroveň kvality ppm (parts-per-million).

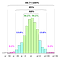
Všechny tyto výpočty vycházejí z implicitního předpokladu, že data populace (NE vzorku) se řídí Gaussovým rozdělením i.Tj. základní proces, z něhož byla všechna data generována (v minulosti i v současnosti), se řídí vzorkem na levé straně.

Ale co se stane, když se data řídí vzorem na pravé straně?“

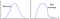
Nebo tohle a… tamto?

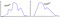
Je nějaká univerzálnější hranice, když data NEJSOU normální?“

Nakonec budeme stejně potřebovat matematicky správnou techniku pro kvantifikaci naší hranice spolehlivosti, i když data nejsou normální. To znamená, že náš výpočet se může trochu změnit, ale stále bychom měli být schopni říci něco takového –

„Pravděpodobnost pozorování nového datového bodu v určité vzdálenosti od průměru je taková a taková…“

Je zřejmé, že musíme hledat univerzálnější hranici, než jsou ctěné Gaussovy hranice 68-95-99. To znamená, že je třeba hledat univerzálnější hranici.7 (odpovídající vzdálenosti 1/2/3 směrodatné odchylky od průměru).

Naštěstí jedna taková hranice existuje a nazývá se „Chebyševova hranice“.

Co je to Chebyshev Bound a k čemu je užitečná?

Chebyshevova nerovnost (nazývaná také Bienaymé-Chebyshevova nerovnost) zaručuje, že pro širokou třídu rozdělení pravděpodobnosti nemůže být více než určitý zlomek hodnot vzdálen od průměru.

Konkrétně, ne více než 1/k² hodnot rozdělení může být vzdáleno od průměru více než k směrodatných odchylek (nebo ekvivalentně, alespoň 1-1/k² hodnot rozdělení je do k směrodatných odchylek od průměru).

Platí prakticky pro neomezený počet typů rozdělení pravděpodobnosti a funguje za mnohem mírnějšího předpokladu než normalita.

Jak to funguje?

I když nevíte nic o tajném procesu, který se skrývá za vašimi daty, je velká pravděpodobnost, že můžete říci následující,

„Jsem si jist, že 75 % všech dat by mělo spadat do 2 směrodatných odchylek od průměru“,

nebo,

Jsem si jist, že 89 % všech dat by mělo spadat do 3 směrodatných odchylek od průměru“.

Tady to vypadá pro libovolně vypadající rozdělení,

Jak to použít?

Jak už asi tušíte, základní mechanika vaší analýzy dat se nemusí ani trochu měnit. Stále budete shromažďovat vzorek dat (čím větší, tím lepší), počítat stejné dvě veličiny, které jste zvyklí počítat – průměr a směrodatnou odchylku, a pak místo pravidla 68-95-99,7 použijete nové meze.

Tabulka vypadá následovně (zde k značí tolik směrodatných odchylek od průměru),

Video ukázka jeho použití je zde,

V čem je háček? Proč lidé tuto „univerzálnější“ vazbu nepoužívají?

Podíváním se na tabulku nebo matematickou definici je zřejmé, v čem je háček. Čebyševovo pravidlo je mnohem slabší než Gaussovo pravidlo ve věci kladení mezí na data.

Sleduje vzorec 1/k² ve srovnání s exponenciálně klesajícím vzorkem pro normální rozdělení.

Například, abyste mohli cokoli ohraničit s 95% spolehlivostí, musíte zahrnout data do 4,5 směrodatné odchylky oproti normálnímu rozdělení. pouze 2 směrodatné odchylky (pro Normální rozdělení).

Ale i tak to může zachránit situaci, když data nevypadají jako Normální rozdělení.

Existuje něco lepšího?

Existuje další ohraničení zvané „Chernoffova ohraničení“/Hoeffdingova nerovnost, které dává exponenciálně ostrý chvost rozdělení (ve srovnání s 1/k²) pro součty nezávislých náhodných veličin.

To lze také použít místo Gaussova rozdělení, když data nevypadají normálně, ale pouze tehdy, když máme vysokou míru jistoty, že základní proces se skládá z dílčích procesů, které jsou na sobě zcela nezávislé.

Naneštěstí v mnoha společenských a obchodních případech jsou výsledná data výsledkem mimořádně komplikované interakce mnoha dílčích procesů, které mohou mít silnou vzájemnou závislost.

Shrnutí

V tomto článku jsme se seznámili s určitým typem statistické vazby, kterou lze použít na nejširší možné rozdělení dat nezávisle na předpokladu normality. To se hodí v případě, že o skutečném zdroji dat víme jen velmi málo a nemůžeme předpokládat, že se řídí Gaussovým rozdělením. Tato mez se řídí mocninným zákonem namísto exponenciálního charakteru (jako Gaussovo), a proto je slabší. Je to však důležitý nástroj, který můžete mít v repertoáru pro analýzu libovolného druhu rozdělení dat.