2.12: Van der Waalsova rovnice

Van der Waalsova rovnice přímočaře rozšiřuje rovnici ideálního plynu. Van der Waalsova rovnice je

\

Vyhovuje údajům o tlaku, objemu a teplotě reálného plynu lépe než rovnice ideálního plynu. Lepšího přizpůsobení se dosáhne zavedením dvou parametrů (označených jako „\(a\)“ a „\(b\)“), které musí být pro každý plyn stanoveny experimentálně. Van der Waalsova rovnice je obzvláště užitečná v naší snaze pochopit chování reálných plynů, protože ztělesňuje jednoduchý fyzikální obraz rozdílu mezi reálným a ideálním plynem.

Při odvozování Boylova zákona z Newtonových zákonů předpokládáme, že molekuly plynu na sebe vzájemně neinteragují. Jednoduché argumenty ukazují, že to může být pravda jen přibližně. Skutečné molekuly plynu na sebe musí vzájemně působit. Na malé vzdálenosti se vzájemně odpuzují. Na poněkud větší vzdálenosti se vzájemně přitahují. Rovnici ideálního plynu lze také odvodit ze základních předpokladů, které jsme uvedli v § 10, aplikací teorie statistické termodynamiky. Na základě různých předpokladů o molekulových vlastnostech můžeme použít statistickou termodynamiku k odvození\({}^{5}\) van der Waalsovy rovnice. Požadované předpoklady jsou, že molekuly zaujímají konečný objem a že se vzájemně přitahují silou, která se mění jako převrácená mocnina vzdálenosti mezi nimi. (Obvykle se předpokládá, že přitažlivá síla je úměrná \(r^{-6}\).)

Abychom si uvědomili, že skutečné molekuly plynu se navzájem přitahují i odpuzují, stačí si uvědomit, že každý plyn lze zkapalnit snížením jeho teploty a zvýšením tlaku, který na něj působí. Pokud kapalinu dále ochladíme, zmrzne na pevnou látku. Dvě charakteristické vlastnosti pevné látky jsou, že si zachovává svůj tvar a že je téměř nestlačitelná. Nestlačitelnost pevné látky přisuzujeme odpudivým silám mezi molekulami, které ji tvoří; ty se k sobě přiblížily natolik, že odpudivé síly mezi nimi nabyly na významu. Chceme-li pevnou látku stlačit, musíme molekuly k sobě ještě více přitlačit, což vyžaduje nepřiměřenou sílu. Na druhou stranu, pokud hodíme kostku ledu přes celou místnost, všechny molekuly vody, které ji tvoří, letí přes celou místnost společně. Je zřejmé, že molekuly vody v pevném tělese se navzájem přitahují, jinak by šly všechny svou cestou – házení kostkou ledu by bylo jako házení hrstí suchého písku. Molekuly vody jsou však stejné molekuly bez ohledu na teplotu nebo tlak, takže pokud mezi nimi v pevné látce existují přitažlivé a odpudivé síly, musí tyto síly působit i v kapalné a plynné fázi.

V plynné fázi jsou molekuly daleko od sebe, v kapalné nebo pevné fázi jsou na sebe nabaleny. Při teplotě varu je objem kapaliny mnohem menší než objem plynu, z něhož je kondenzována. Při bodu tuhnutí se objem pevné látky jen nepatrně liší od objemu kapaliny, z níž zmrzla, a je určitě větší než nula. Tato běžná pozorování lze snadno vysvětlit předpokladem, že každá molekula má charakteristický objem. To zase můžeme chápat jako důsledek povahy mezimolekulárních sil; je zřejmé, že tyto síly sílí s klesající vzdáleností mezi dvojicí molekul. Protože kapalina nebo pevná látka zaujímá určitý objem, musí se odpudivá síla zvětšovat rychleji než přitažlivá síla, když je mezimolekulární vzdálenost malá. Často je užitečné hovořit o molárním objemu kondenzované fáze. Molárním objemem rozumíme objem jednoho molu čisté látky. Molární objem kondenzované fáze je určen mezimolekulovou vzdáleností, při které existuje rovnováha mezi mezimolekulovými přitažlivými a odpudivými silami.

Je zřejmé, že v kondenzovaných fázích jsou molekuly velmi blízko sebe. Předpokládáme-li, že prázdné prostory mezi molekulami jsou zanedbatelné, je objem kondenzované fáze přibližně roven počtu molekul ve vzorku vynásobenému objemem jedné molekuly. Molární objem je pak Avogadrovo číslo vynásobené objemem, který zaujímá jedna molekula. Známe-li hustotu, D, a molární hmotnost, \(\overline{M}\), můžeme zjistit molární objem, \(\overline{V}\), jako

\

Objem obsazený jednou molekulou, V\({}_{molekula}\), je

\

Tlak a objem, které se objevují ve van der Waalsově rovnici, jsou tlak a objem skutečného plynu. Výrazy ve van der Waalsově rovnici můžeme vztáhnout k rovnici ideálního plynu: Je užitečné považovat výrazy \(\left(P+{{an}^2}/{V^2}\right)\) a \(\left(V-nb\right)\) za tlak a objem hypotetického ideálního plynu. To znamená

\ &=nRT \end{align*}\]

Tedy máme

\

Rovnici ideálního plynu odvodíme z modelu, ve kterém jsou molekuly neinteragující bodové hmoty. Objem ideálního plynu je tedy objem, který zaujímá plyn, jehož jednotlivé molekuly mají nulový objem. Jestliže jednotlivé molekuly reálného plynu efektivně zaujímají objem \({b}/{\overline{N}}), pak \(n\) jejich molekul efektivně zaujímá objem

\

Van der Waalsova rovnice říká, že objem reálného plynu je objem, který by zaujímaly neinteragující bodové hmoty, \(V_{ideální plyn}\), plus efektivní objem samotných molekul plynu. (Při dosazování údajů o molekulách skutečného plynu do van der Waalsovy rovnice je hodnota \(b\) obvykle o něco větší než objem odhadnutý z hustoty kapaliny a molekulové hmotnosti. Viz úloha 24.)

Podobně máme

\

Můžeme to chápat jako logický důsledek přitažlivých interakcí mezi molekulami reálného plynu. S \(a>0\) říká, že tlak skutečného plynu je menší než tlak hypotetického ideálního plynu o množství, které je úměrné \({\levice({n}/{V}\pravice)}^2\). Konstanta úměrnosti je \(a\). Protože \({n}/{V}\) je molární hustota (molekuly na jednotku objemu) molekul plynu, je to míra koncentrace. Počet srážek mezi molekulami stejného druhu je úměrný čtverci jejich koncentrace. (Podrobněji se tímto bodem zabýváme v kapitolách 4 a 5.) \({\left({n}/{V}\right)}^2\) je tedy mírou četnosti, s jakou se skutečné molekuly plynu dostávají do těsného vzájemného kontaktu. Pokud se při vzájemném přiblížení přitahují, měl by být účinek této přitažlivosti úměrný \({\left({n}/{V}\right)}^2\). Van der Waalsova rovnice je tedy v souladu s myšlenkou, že tlak skutečného plynu se liší od tlaku hypotetického ideálního plynu o hodnotu, která je úměrná četnosti a síle přitažlivých interakcí.

Proč by ale měly mít přitažlivé interakce tento účinek; proč by měl být tlak skutečného plynu menší než tlak hypotetického ideálního plynu? Snad nejlepším způsobem, jak si vytvořit kvalitativní představu, je uvědomit si, že přitažlivé mezimolekulární síly mají tendenci způsobovat shlukování molekul plynu. Koneckonců jsou to právě tyto přitažlivé sílypřitažlivé síly, které způsobují shlukování molekul do kapaliny při nízkých teplotách. Nad bodem varu schopnost molekul plynu jít svou cestou omezuje účinky této tendence, nicméně i v plynu musí přitažlivé síly působit tak, že mají tendenci zmenšovat objem, který molekuly zaujímají. Protože objem obsazený plynem je dán velikostí nádoby – nikoliv vlastnostmi samotného plynu – nachází tato tendence ke shlukování vyjádření v podobě poklesu tlaku.

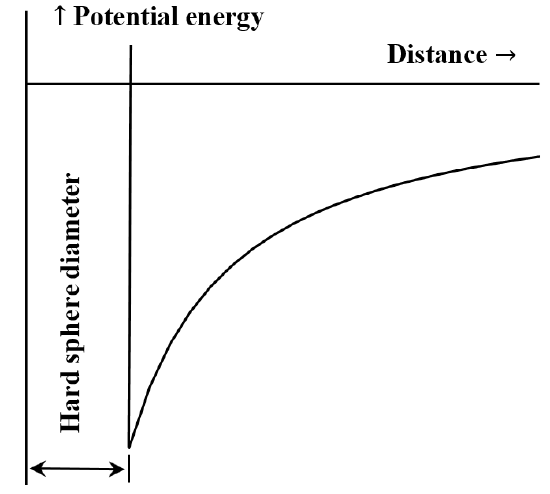
Často je užitečné popsat interakci mezi částicemi nebo chemickými částicemi pomocí diagramu potenciální energie v závislosti na vzdálenosti. Van der Waalsova rovnice odpovídá případu, kdy odpudivá interakce mezi molekulami neexistuje, dokud se molekuly nedostanou do kontaktu. Jakmile se dostanou do kontaktu, energie potřebná k jejich ještě většímu přiblížení se stává libovolně velkou. Často se to popisuje slovy, že se chovají jako „tvrdé koule“. Přitažlivá síla mezi dvěma molekulami klesá s rostoucí vzdáleností mezi nimi. Když jsou od sebe velmi daleko, je přitažlivá interakce velmi malá. Říkáme, že energie interakce je nulová, když jsou molekuly nekonečně daleko od sebe. Máme-li zpočátku dvě široce oddělené, nehybné, vzájemně se přitahující molekuly, budou se samovolně pohybovat směrem k sobě, přičemž budou získávat kinetickou energii. Jejich potenciální energie klesá s tím, jak se k sobě přibližují, a nejmenší hodnoty dosáhne, když se molekuly setkají. Z van der Waalsovy rovnice tedy vyplývá diagram závislosti potenciální energie na vzdálenosti, který je nakreslen na obrázku 5.

.