Circunferência de um Círculo – Explicação & Exemplos
On Janeiro 21, 2022 by adminVimos antes como encontrar o perímetro do polígono. Sabemos que o círculo não é um polígono, portanto, não deve ter um perímetro. Usamos uma forma equivalente para um círculo, chamada circunferência.
Neste artigo, vamos discutir como encontrar a circunferência de um círculo, a fórmula da circunferência de um círculo e exemplos de problemas sobre a circunferência de um círculo.
Qual é a circunferência de um círculo?
A distância em torno de um polígono tal quadrado ou retângulo é chamado de perímetro (P). Por outro lado, a distância ao redor de um círculo é chamada de circunferência (C). Portanto, a circunferência de uma circunferência é a distância linear de uma aresta da circunferência.
Por que precisamos de calcular a circunferência de uma circunferência?
Deve-se encontrar a circunferência de um objecto nos seguintes cenários:
Se quiser comprar um soutien, uma calça ou uma camisola, precisa de saber a distância à volta da cintura ou do peito. Embora seu corpo não seja um círculo perfeito, você terá que medir sua circunferência usando uma fita métrica. Alfaiates usam principalmente esta técnica para determinar a circunferência de um vestido.
Você também precisa saber a circunferência de um círculo fazendo trabalhos artesanais, colocando esgrima ao redor de sua banheira, ou apenas resolvendo um problema de matemática para a escola.
Como encontrar a circunferência de um círculo?
Como dito anteriormente, o perímetro ou circunferência de um círculo é a distância ao redor de um círculo ou qualquer forma circular. A circunferência de uma circunferência é a mesma que o comprimento de uma linha reta que é dobrada ou dobrada para fazer a circunferência. A circunferência de uma circunferência é medida em metros, quilómetros, jardas, polegadas, etc.
Há duas maneiras de encontrar o perímetro ou circunferência de uma circunferência. A primeira fórmula envolve a utilização do raio e a segunda envolve a utilização do diâmetro de uma circunferência. É importante notar que, os dois métodos produzem o mesmo resultado.
Vamos dar uma olhada.
A circunferência de uma circunferência é dada por;
C = 2 * π* R = 2πR
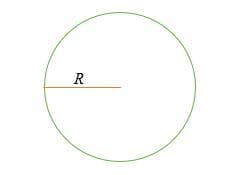
where,
C = Circunferência ou perímetro,
R = o raio de uma circunferência,
π = a constante matemática conhecida como Pi
Or
C = π* D = π D
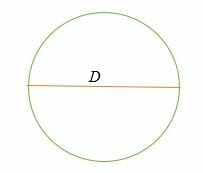
where, D = 2R = O diâmetro de um círculo
Para qualquer círculo, a razão entre a sua circunferência e o seu diâmetro é igual a uma constante conhecida como pi.
Circunferência/Diametro = Pi
C /D = Pi ou C/2R = pi
O valor aproximado de pi (π) = 22/7 = 3,1415926535897…. (um valor sem terminação)
Para facilitar o cálculo da circunferência de um círculo, o valor de pi é tomado como 3,14 (π = 3,14).
Vejamos alguns exemplos abaixo para polir o conceito de circunferência.
Exemplo 1
Ponhamos a circunferência da circunferência com um raio de 8 cm.
Solução
Circunferência = 2 * π* R = 2πR
= 2 * 3.14 * 8
= 50.24 cm.
Exemplo 2
Calcular a circunferência de um círculo cujo diâmetro é 70 mm
Solução
Circunferência = π* D = π D
= 3,14 * 70
= 219.8 mm
Exemplo 3
Calcular o perímetro de um jardim circular de flores cujo raio é de 10 m.
Solução
Circunferência = 2 * π* R = 2πR
= 2 * 3.14 * 10
= 62.8 m.
Exemplo 4
A circunferência de um círculo é de 440 jardas. Encontrar o diâmetro e raio da circunferência.
Solução
Circunferência = 2 * π* R = 2πR
440 =2 * 3.14 * R
440 = 6.28R
Dividir ambos os lados por 6,28 para obter,
R = 70,06
Por isso, o raio do círculo é de 70,06 jardas. Mas, como o diâmetro é o dobro do raio de uma circunferência, então, o diâmetro é igual a 140,12 jardas.
Exemplo 5
O diâmetro das rodas de uma bicicleta é 100 cm. Quantas rotações cada roda fará para percorrer uma distância de 157 metros
Solução
Calcular circunferência da roda da bicicleta.
Circunferência = π D
= 3.14 * 100
= 314 cm
Para obter o número de rotações da roda, divida a distância coberta pela circunferência da roda.
Precisamos converter 157 metros para cm antes de dividir, então multiplicamos 157 por 100 para obter 15700 cm. Portanto,
Número de rotações = 15700 cm/314 cm
= 50 rotações.
Exemplo 6
Um pedaço de fio na forma de um retângulo de 100 cm de comprimento e 50 cm de largura é cortado e dobrado para fazer um círculo. Calcular a circunferência e o raio da circunferência formada.
Solução
A circunferência da circunferência formada = o perímetro do fio rectangular.
Perímetro de um rectângulo = 2(L + W)
= 2(100 + 50) cm
= 2 * 150 cm
= 300 cm.
Por isso, a circunferência da circunferência será de 300 cm.
Calcular agora o seu raio.
Circunferência = 2 π R
300 cm = 2 * π * R
300 cm = 2 * 3.14 * R
300 cm = 6.28R
Dividir ambos os lados por 6.28.
R = 47.77 cm
Então, o raio do círculo será 47,77 cm.
Exemplo 7
O raio de cada roda de uma motocicleta é 0. 85 m. Até onde se moverá o motociclo se cada roda fizer 1000 rotações. Suponha que a motocicleta está se movendo em linha reta.
Solução
Primeiro, encontre a circunferência da roda.
Circunferência = 2 π R
= 2 * 3.14 * 0.85
= 5.338 m.
Para encontrar a distância percorrida, multiplique a circunferência da roda pelo número de rotações tomadas.
Distância = 5,338 * 1000
= 5338 m
Por isso, a distância percorrida é igual a 5,338 quilómetros.
Perguntas Práticas
- Uma pizza de 12 polegadas é servida ao Mike e aos seus amigos. Mike está interessado em calcular a sua circunferência. Ajude-o!
- O perímetro de um determinado quadrado é de 1/3 da área de um determinado círculo. Se o comprimento do quadrado for L unidades, determine o diâmetro do círculo em termos de L.
Respostas
- 12π polegadas ou 37,67 polegadas
- 12L/π unidades
Deixe uma resposta