2.12: Equação de Van der Waals

Uma equação devido a van der Waals estende a equação de gás ideal de uma forma simples. A equação de Van der Waals é

A equação de Van der Waals é

A equação de Van der Waals é melhor para um gás real do que a equação de gás ideal. O ajuste melhorado é obtido pela introdução de dois parâmetros (designados por “a” e “b”)) que devem ser determinados experimentalmente para cada gás. A equação de Van der Waals é particularmente útil em nosso esforço para entender o comportamento dos gases reais, pois ela incorpora um quadro físico simples para a diferença entre um gás real e um gás ideal.

Na derivação da lei de Boyle das leis de Newton, assumimos que as moléculas de gás não interagem umas com as outras. Argumentos simples mostram que isto só pode ser aproximadamente verdade. Moléculas de gás reais devem interagir umas com as outras. A curtas distâncias, elas se repelem umas às outras. A distâncias um pouco mais longas, elas se atraem umas às outras. A equação ideal de gás também pode ser derivada das suposições básicas que fazemos no §10 por uma aplicação da teoria da termodinâmica estatística. Fazendo diferentes suposições sobre propriedades moleculares, podemos aplicar a termodinâmica estatística para derivar a equação de van der Waals (5). As suposições necessárias são que as moléculas ocupam um volume finito e que elas se atraem umas às outras com uma força que varia como o inverso de um poder da distância entre elas. (A força atrativa é geralmente assumida como proporcional a ^(r^{-6}})

Para reconhecer que moléculas reais de gás tanto atraem como se repelem, basta lembrar que qualquer gás pode ser liquefeito reduzindo sua temperatura e aumentando a pressão aplicada a ele. Se resfriarmos ainda mais o líquido, ele congela até um sólido. Agora, duas características distintivas de um sólido são que ele mantém a sua forma e que é quase incompressível. Atribuímos a incompressibilidade de um sólido às forças repulsivas entre suas moléculas constituintes; elas se aproximaram tanto uma da outra que as forças repulsivas entre elas se tornaram importantes. Para comprimir o sólido, as moléculas devem ser empurradas ainda mais próximas umas das outras, o que requer uma força desordenada. Por outro lado, se atirarmos um cubo de gelo através da sala, todas as moléculas de água que as compõem voam juntas através da sala. Evidentemente, as moléculas de água no sólido são atraídas umas pelas outras, caso contrário, todas elas seguiriam caminhos separados – atirar o cubo de gelo seria como atirar um punhado de areia seca. Mas as moléculas de água são as mesmas moléculas qualquer que seja a temperatura ou pressão, então se há forças de atração e repulsão entre elas no sólido, essas forças devem estar presentes nas fases líquida e gasosa também.

Na fase gasosa, as moléculas estão muito separadas; na fase líquida ou sólida, elas estão empacotadas juntas. No seu ponto de ebulição, o volume de um líquido é muito inferior ao volume do gás do qual ele é condensado. No ponto de congelamento, o volume de um sólido é apenas ligeiramente diferente do volume do líquido a partir do qual é congelado, e é certamente maior que zero. Estas observações comuns são prontamente explicadas supondo que qualquer molécula tem um volume característico. Podemos entender isto, por sua vez, como uma consequência da natureza das forças intermoleculares; evidentemente, estas forças tornam-se mais fortes à medida que a distância entre um par de moléculas diminui. Como um líquido ou um sólido ocupa um volume definido, a força repulsiva deve aumentar mais rapidamente do que a força atrativa quando a distância intermolecular é pequena. Muitas vezes é útil falar sobre o volume molar de uma fase condensada. Por volume molar, entendemos o volume de uma molécula de uma substância pura. O volume molar de uma fase condensada é determinado pela distância intermolecular na qual há um equilíbrio entre as forças intermoleculares de atração e repulsão.

As moléculas são muito próximas umas das outras em fases condensadas. Se supomos que os espaços vazios entre as moléculas são insignificantes, o volume de uma fase condensada é aproximadamente igual ao número de moléculas na amostra multiplicado pelo volume de uma única molécula. Então o volume molar é o número de Avogadro vezes o volume ocupado por uma molécula. Se conhecermos a densidade, D, e a massa molar, D, e a massa molar, M, podemos encontrar o volume molar, V, como

O volume ocupado por uma molécula, V\({}_molecule}), torna-se

A pressão e o volume que aparecem na equação de van der Waals são a pressão e o volume do gás real. Podemos relacionar os termos na equação de van der Waals com a equação do gás ideal: É útil pensar nos termos P+2 (esquerda) e V+2 (direita) como a pressão e o volume de um gás ideal hipotético. Isto é

&=nRT {alinhamento*}]

Então temos

>

Derivamos a equação de gás ideal de um modelo em que as moléculas são massas de ponto não-interactivo. Então o volume de um gás ideal é o volume ocupado por um gás cujas moléculas individuais têm volume zero. Se as moléculas individuais de um gás real efetivamente ocupam um volume, então moléculas delas efetivamente ocupam um volume

A equação de Van der Waals diz que o volume de um gás real é o volume que seria ocupado por massas de pontos não interativos, mais o volume efetivo das próprias moléculas de gás. (Quando os dados das moléculas de gás reais se encaixam na equação de van der Waals, o valor de b) é geralmente um pouco maior do que o volume estimado a partir da densidade líquida e do peso molecular. Ver problema 24.)

Simplesmente, temos

>

Possibilitamos entender isto como uma consequência lógica das interacções atractivas entre as moléculas do gás real. Com {\i1}(a>0}), diz que a pressão do gás real é menor que a pressão do hipotético gás ideal, por uma quantidade que é proporcional a {\i}(esquerda(n}/{V}direita)^2}. A constante de proporcionalidade é… Como a densidade molar (moles por unidade de volume) das moléculas de gás é a densidade molar (moles por unidade de volume), é uma medida de concentração. O número de colisões entre moléculas do mesmo tipo é proporcional ao quadrado da sua concentração. (Consideramos este ponto com mais detalhes nos Capítulos 4 e 5.) Portanto, {{esquerda(n}/{V}direita)^2} é uma medida da frequência com que as moléculas reais de gás entram em contato próximo umas com as outras. Se elas se atraem umas às outras quando se aproximam, o efeito desta atracção deve ser proporcional ao da esquerda/direita2). Então a equação de van der Waals é consistente com a idéia de que a pressão de um gás real é diferente da pressão do gás ideal hipotético por uma quantidade que é proporcional à freqüência e força das interações atrativas.

Mas por que interações atrativas deveriam ter esse efeito; por que a pressão do gás real deveria ser menor do que a do gás ideal hipotético? Talvez a melhor maneira de desenvolver um quadro qualitativo seja reconhecer que forças intermoleculares atraentes tendem a fazer com que as moléculas de gás se aglomerem. Afinal, são essas forças atraentes que causam a agregação das moléculas a um líquido a baixas temperaturas. Acima do ponto de ebulição, a capacidade das moléculas de gás de seguirem caminhos separados limita os efeitos desta tendência; no entanto, mesmo no gás, as forças atrativas devem agir de uma forma que tende a reduzir o volume ocupado pelas moléculas. Como o volume ocupado pelo gás é ditado pelo tamanho do recipiente – e não pelas propriedades do gás em si – esta tendência de aglomeração se expressa como uma diminuição da pressão.

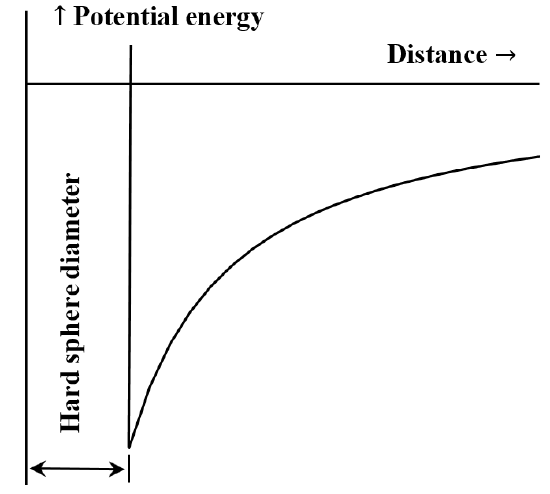
É frequentemente útil descrever a interacção entre partículas ou moieties químicas em termos de um diagrama de energia potencial versus distância. A equação de van der Waals corresponde ao caso de que a interação repulsiva entre moléculas é inexistente até que as moléculas entrem em contato. Uma vez que elas entram em contato, a energia necessária para movê-las ainda mais próximas umas das outras torna-se arbitrariamente grande. Muitas vezes isso é descrito dizendo que elas se comportam como “esferas duras”. A força de atracção entre duas moléculas diminui à medida que a distância entre elas aumenta. Quando elas estão muito distantes, a interação atrativa é muito pequena. Nós dizemos que a energia da interação é zero quando as moléculas estão infinitamente distantes. Se inicialmente tivermos duas moléculas amplamente separadas, estacionárias e mutuamente atraentes, elas se moverão espontaneamente em direção uma à outra, ganhando energia cinética à medida que se afastam. A sua energia potencial diminui à medida que se aproximam uma da outra, atingindo o seu menor valor quando as moléculas entram em contacto. Assim, a equação de van der Waals implica o diagrama de energia potencial versus distância esboçado na Figura 5.